@davidlkl From the profit distribution plot, it looks like you don’t have any claim with 10K+ profit. It looks like our code ended up with nan as the array was empty.
OK so that’s helpful to know nan% is a possible output. So as in week 9 I got 100% in the “never x 10k+” claims heatmap cell it means there were some policies in the market that had claims in the 10k+ range.
I haven’t really changed my claim model for the last 5 weeks or so. All I’ve been doing is tweaking pricing strategy, gradually edging rates up. When there have been large 50k capped claims in the market historically I’ve been rather good at writing them and therefore ended up with a low leaderboard position. When, I suspect, there haven’t been many large losses (week 5 and 9 ?) I end up in a reasonable leaderboard position (1st and 3rd).
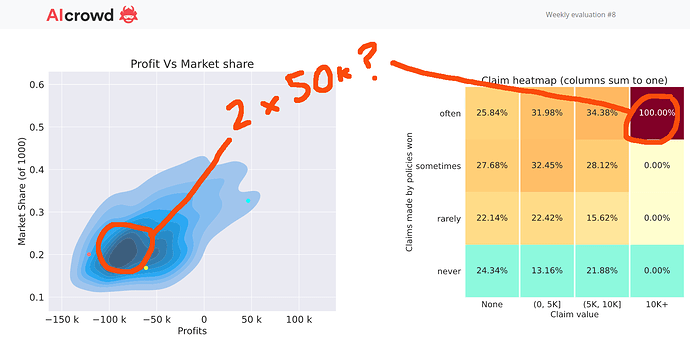
I’d be really interested to know if anyone thinks there were any 50k capped losses in this round. Sometimes you can tell because your profit exhibit is centered around -50k or -100k and the claims heatmap exhibit will say 100% in the “often x 10k+” cell.
Like my week 8 chart…
If there were 50K claims and I avoided them then maybe I’ve found the right level of premium loading to claims. More likely though that my margin is too high now, given my small market share, and I’ve got lucky on the policies I did write.
Thanks for the reply. But Nigel has never got a claim size of 10k shouldnt it be nan for his as well?
Hi @davidlkl
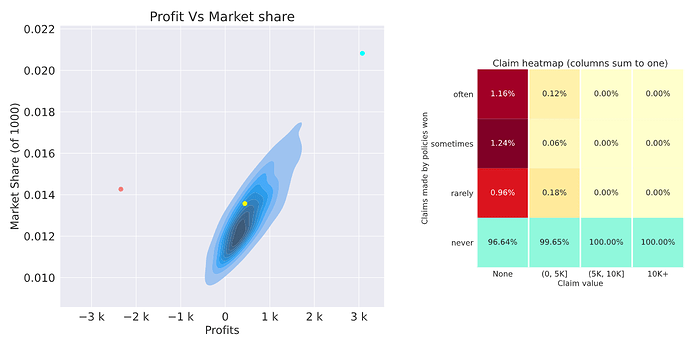
Yeah the nan is a bit weird, and we’ll look into it. There were claims of 10K+ this week in the data so you should not have received a nan. It should have looked like Nigel’s plot. 
We’ll investigate and see what’s going on 
Here’s my feedback this time around (also no 10k+ claims). After seeing the market share column in last week’s feedback, it seemed like going after a small market share was a strategy that would get us to the upper 25th percentile of the market, which is much better than my team was doing previously. It worked… we have a profit of $465 now.
If I look at the week 9 top ranked profit participants who have a sizable market share and haven’t changed their models in a while, their ranking looks to have a lot of luck involved.
For example, @etienne_arbogast (#2) with 36% market share:

And @evanpetzoldt (#7) with 25% market share:
On the other hand, @nick_corona with <1% market share has consistently done respectably well:
So, I guess maybe the takeaway is that if many top 10 percentile (competitive models) are shooting for small market shares or niche markets, then that the models that are left over will soak up the rest. Because there isn’t really a great way to figure out which markets the niche players are targeting, the rest will have a lot of unpredictable variability. And, because the niche players are targeting such small market shares, there are plenty of profits to be had elsewhere, so potentially the top few will be quite random.
What are other people’s thoughts? Is anyone else shocked at how high the profit loads are needed to get to profitability??? The profit loads we had to apply to get to profitability is mind blowing to me. 
Obviously I’m curious if anyone has found a strategy that consistently wins a reasonable market share and is profitable, however I doubt those players will share right now. Hopefully after this competition, someone (maybe @alfarzan  ) writes a thesis paper on this.
) writes a thesis paper on this.
These NaN are very strange…
I think (as pointed out by @nigel_carpenter) the results are very sensitive to the large claims…
On my side the last week results indicate one large claim around 15K that I got (relatively) often :
It also looks like the conversion rate still varies a lot (so the prices haven’t stabilized yet).
I have a question for @alfarzan: can you confirm the number of policies in the often, sometimes and rarely is the same ? I don’t understand how I got this split if that’s the case  …
…
Just to confirm, each of the rows (excluding the “never” row) sum up to roughly the same number of policies as they are quantiles (the same as the rows on the tables below).
@guillaume_bs what is the confusion on that point? Is it something I can help clarify?
@lolatu2 actually the hope is that we’ll be able to provide the community with those insights a few weeks after the end of the competition during an online event anyone can join and contribute to! That’s not only to save you from having to read my thesis.
Thanks @alfarzan for confirming.
Here what puzzles me is that on all claims segments the “often” figures are much higher than the “rarely” ones. I don’t think these figures would be possible with the same number of policies in each row.
Ah I see, I think I understand.
So these column normalised, meaning columns sum to 100%. So the heatmap is telling you about the wider market and your performance within it.
Toy example with 10K policies 
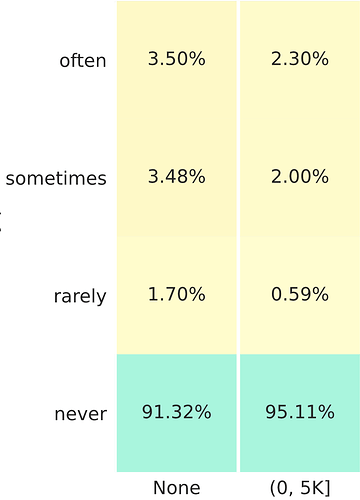
Let’s take a toy example where there are a total of 10K policies in the whole dataset, and and we only have two columns, the None (A) and the (0, 5K] (B). Further let’s say they’re broken down such that.
Column A. 9K contracts
Column B. 1K contracts
So what do the numbers in your heatmap mean?
How many policies does each row represent? 
First let’s see how many policies you win with any frequency:
Column A. We know that 91.32% of these you never win. That means you win 8.68% of them in some situation. That’s 0.0868 x 9000 = 7821 policies. Split equally among the three rows that’s ~ 2600 policies per cell (excluding never)
Column B. Similarly for this column you will sometimes win 0.0489 x 1000 = 489 policies. That’s ~160 per cell
So what do the percentage numbers mean? 
This heatmat is telling you how exposed you are to the entire market with the view on claim amounts.
Ok so what does it mean to say for the column A policies, you have 3.5% in the top cell? That means that the policies that you win often and don’t make a claim (~2600 policies), represent 3.5% of the entire set of policies that don’t make a claim in the market.
Similarly in column B, the top row with 2.3% means, that the policies you win often and have a claim less than 5K (~160 policies) represent 2.3% of all the policies that have made a claim in that range in the market.
I hope that makes it clearer  (and that my maths is correct!)
(and that my maths is correct!)
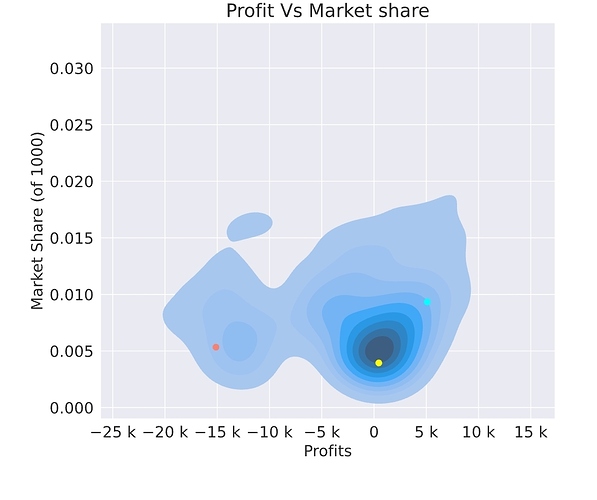
Indeed it looks like the this week we have avoided larger claims. The two competitors at the very bottom of the leaderboard are giving us the weekly summary statistics.
Special prize for an explanation of mkeywood’s “profit” at 0.9% market share!
Haha 
I would feel it is not my place to reveal the strategy of @mkeywood on this one, but I did look into it to see what is going on.
Genuinely I have no idea what happened there. I was 4th last week, and then this abominable result this week, BUT I have not seen any leaderboard feedback for week 8 or 9 (ie, at all) so I have been fishing in the dark  )
)
Anyone who can help explain it to me, i’d be happy 
Ah your feedback is actually on the submission itself.
If you go to the leaderboard, click on “view” next to your leaderboard submission and then navigate to the “evaluation status” tab you will see the feedback 
I think I may have joined this challenge a little late (week 8) to really get a handle on it, but I hope they do more like this. Adding this pricing aspect is way way more interesting than just claim model prediction 
Thanks @alfarzan for your explanation, but I must say I am still a bit lost.
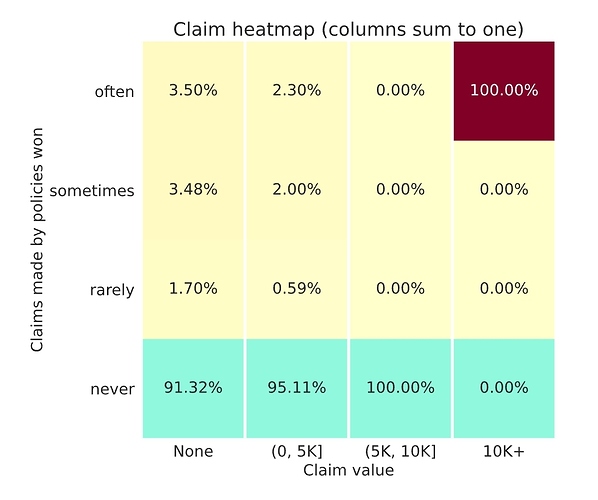
Taking your toy example with 10K claims, with a 10% frequency, and ignoring the last 2 columns which are very rare.
- The policies won “often” represent 3.5% of the policies with no claims - around 3.5% x 9K = 315 - plus 2.3% of the policies with a small claim - around 2.3% x 1K = 23 - so the total here is around 338.
- The policies won “rarely” represent 1.7% of the policies with no claims - around 1.7% x 9K = 153 - plus 0,59% of the policies with a small claim - around 0.6% x 1K = 6 - so the total there is around 159.
There are some approximations here, but overall, as the two values for “often” are larger than both values for “rarely” I don’t see any solution where the number of policies are equal… so I might be misinterpreting the heatmap somehow 
I have the same confusion as yours too.
If the number of policies is equally split among [often, sometimes and rarely] (the nominator), and the fractions are different, the denominator must be different.
My guess on why high profit loads are required:
As the (top 10) competitors are becoming niche and better, it is more likely for us to pick up underpriced policies, therefore apply a higher profit load protect us against it. All in all, if we have a super high profit load and not winning many policies, our profits will be close to 0 and enough to beat many other competitors. In other words, to beat the top and niche player, we need to be niche as well!
Ahh ok I see what you (and @davidlkl) originally meant now.
The answer is not going to be very satisfying I’m afraid: these are small measurement errors.
In reality when we have to construct the quantiles, it’s not always exactly equal and we have to allow the algorithm some leeway to make things approximately equal. When the market share is very low, when we are contructing these buckets, that error becomes relatively large. Hence the issue you observe.
I’m attaching another feedback with a average marketshare of ~0.05 so you can see that the numbers become closer when the buckets are constructed using more inputs.
Here assuming claim frequency of each category being 10% of the last.
In this case we have:
- Often. 9000 x 0.04 + 900 x 0.08 + 90 x 0.12 + 10 x 0.3 ~ 446
- Rarely. 9000 x 0.04 + 900 x 0.07 + 90 x 0.08 + 10 x 0 ~ 430
Again not exactly equal but approximately similar