Hey there!
I spent the week venturing deeper and deeper in the pricing strategy…
…
Chaising tail 
def. To be very busy or working very hard at some task but accomplishing little or nothing as a result; to be engaged in some fruitless or futile task or endeavor. (1)
^^ This is what it felt like, throughout the whole week.
You can try all your best, apply various assumptions, and run thousands of simulation.
The missing element is immediate validation, which unfortunately only comes once a week.
I wish there was a better way! 
Hundred hours of CPU time… 


- 11 models (A to L) , all different algorithms.
- All were deemed reasonable fit, in terms of RMSE.
- Fitted 8 different times (a new seed each time S_ ).
- Keeping a different 30% holdout each time.
Profit rank 
For each fit, models are competition, and profit rank returned.
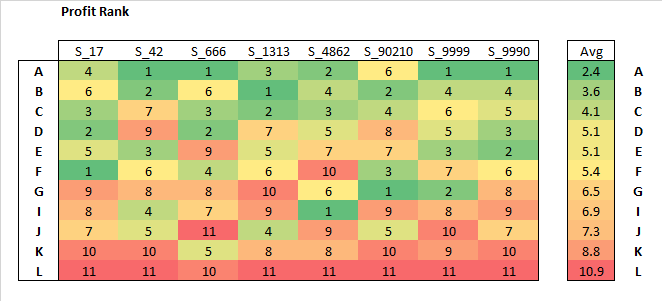
On a profit ranking, as you can see, some models do perform better on average than others.
However, no unilateral better model.
Selecting an average of model A, B, C seems reasonable.
Model L systematically performs the worst.
Safe to say I would never use that model, … right?
Mind blown 
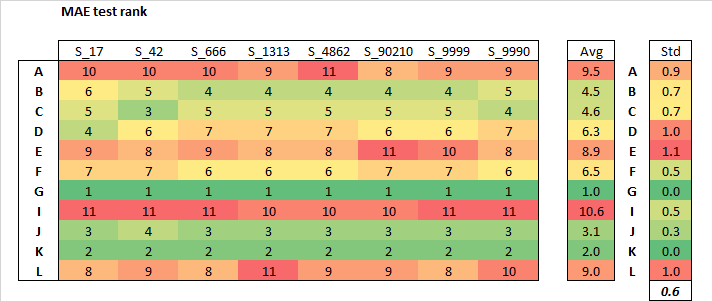
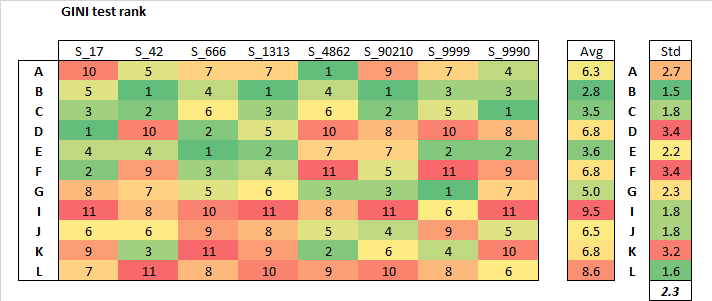
When I put together a similar chart, with a RMSE rank on the holdout test…
EDIT :: CHART WAS IN ERROR, PLEASE SEE MY REPLY BELOW
And the same chart, but on MAE…
EDIT :: CHART WAS IN ERROR, PLEASE SEE MY REPLY BELOW
Siren song 
^ That’s a popular saying in french.
Those two metrics graph lead me to think one can be greatly misled by selecting a model based on RMSE and or MAE.
Coincidently, @lolatu2 did a post recently, questioning if RMSE was an appropriate metric.
And you? 
- What do you all think of this?
- Have you been selecting your best model, based solely on a specific metric? If so, which one?
- Ideally, one would like a metric that is correlated with profit ranking.
- Do you have a metric suggestion that you want me to try?

 .
. )
)


 margin sensitivity
margin sensitivity